Block Compressed Sparse Row (BSR) Matrix Format

BSR is format storage sparse matrix, mainly used in intel MKL solver. Uniform blocks are spilted in original matrix and the zero-blocks and non-zero-blocks are exactly in the blocks. NOTED THAT, the dimension of original matrix must be the integer multiple of the block dimension, ensuring the matrix can be spilt uniformly.

Here’s an example to explain BSR

$$
D=
\begin{pmatrix}
1 & 0 & 6 & 7 & * & * \
2 & 1 & 8 & 2 & * & * \
1 & * & 1 & 4 & * & * \
1 & * & 5 & 1 & * & * \
1 & * & 4 & 3 & 7 & 2 \
1 & * & 0 & 0 & 0 & 0
\end{pmatrix}
$$

1 & 0 & 6 & 7 & * & * \
2 & 1 & 8 & 2 & * & * \

& * & 1 & 4 & * & * \
& * & 5 & 1 & * & * \
& * & 4 & 3 & 7 & 2 \
& * & 0 & 0 & 0 & 0 \
For example, assuming the size of block is 2.

1
2
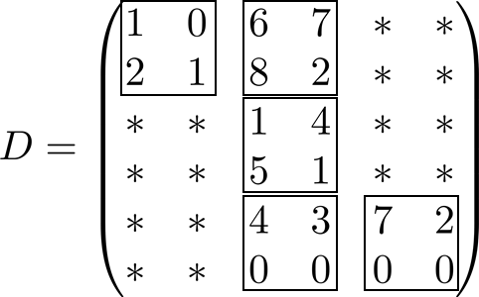
3

values=[1 0 2 1 6 7 8 2 1 4 5 1 4 3 0 0 7 2 0 0]
columes=[0 1 1 1 2]
rowIndex=[0 2 3 5]

Values
A real array that contains the elements of the non-zero blocks of a sparse matrix. The elements are stored block-by-block in row-major order. A non-zero block is the block that contains at least one non-zero element. All elements of non-zero blocks are stored, even if some of them is equal to zero. Within each non-zero block elements are stored in column-major order in the case of one-based indexing, and in row-major order in the case of the zero-based indexing.

columns
Element i of the integer array columns is the number of the column in the block matrix that contains thei-th non-zero block.

rowIndex

Total blocks amount previous block-row i.

rowIndex[i+1]-rowIndex[i]=Block Num in block-row i

Reference:
block compressed sparse row (BSR) matrix format
稀疏矩阵的主要存储格式
 Sparse Matrix Compression Formats
稀疏矩阵的存储格式（Sparse Matrix Storage Formats）

FRIENDS